Project Notes.

If you’re like most people, you want to know how to simulate a Hammond B-3 organ using fixed-point arithmetic on an 8-bit microcontroller.

First, you’re going to need tone generators. In a Hammond, this is a set of 91 tonewheels. Each is positioned adjacent to an electromagnetic pickup, inducing a sinusoidal current at a specific frequency. On a microcontroller, we can simulate the tonewheel assembly with a set of 91 sine oscillators. Take a look at bleep bloop for direct digital synthesis, one method of sine wave generation. We’ll be using it below.

A B-3 has two keyboards, called manuals on an organ. When you press a key, nine of these oscillators connect to the audio output. Each corresponds to a note that’s harmonically related to the key you pressed (including that key’s note, the fundamental). They’re played at volumes set by nine drawbars.

Drawbar	Harmonic	Interval
1	Sub-Fundamental	Sub-Octave
2	Sub-Third	Sub-Third
3	Fundamental	Unison
4	2nd	Octave
5	3rd	12th
6	4th	15th
7	5th	17th
8	6th	19th
9	8th	22nd

So to simulate a Hammond organ, all you need is 91 sine wave oscillators, harmonic ratios to calculate which oscillators apply to each key, and a mixer that can add oscillator outputs together based on the drawbar settings.

It’s that simple!

It’s not that simple.

First, you need to account for harmonic foldback. There aren’t enough tonewheels to play the nine harmonics of every key, and on either end of the manual some tonewheels sound on multiple drawbars. This is no big deal, you just need to handle it in your key->tonewheels mapping.

Second, there’s a phenomenon called key click. On a Hammond, this is a discontinuity in organ output as tonewheels switch in and out of the mix. We get something very similar if we aren’t careful about discontinuities in our DAC output. Great! The lazy programmer wins.

Third, a few of the tonewheels on a Hammond don’t make sine waves — the lowest 12 make more of a square wave tone. Luckily for us, it is even easier to generate square waves. It’s the same frequency calculation, but we can use the highest bit of our accumulator instead of the sine lookup table. These tonewheels are only active on the Hammond’s bass pedal board, so it’s not a big deal if you’re not planning to emulate that.

Fourth, there’s a feature on the Hammond called percussion. This disables one of the drawbars (the 2nd or 3rd harmonic) and plays the associated tonewheel briefly at the beginning of a note. In modern synth terms, this is a single triggered effect — it is only activated when you depress the first key from an all-keys-up state. For percussion, play that tonewheel at slightly increased volume with a quick decay to nothing.

Fifth, many Hammond organs have two built-in effects: chorus and vibrato. Each is available at three intensities, though always at a fixed rate of 7 Hz. We may get into this in the future.

Sixth, you have harmonic leakage. The tonewheels on a Hammond are organized in pairs, and each wheel can induce a small current in its twin. They’re organized so each pair has two tonewheels exactly four octaves apart, so the harmonic impact of leakage is low, but it’s an important part of the Hammond sound.

Seventh, the tonewheels don’t output at the same level. High frequency tones sound louder to us than low frequencies, and the Hammond attempts to keep perceived volumes the same by attenuating the high frequencies more.

Eighth and most critical is the Leslie rotating speaker cabinet. A rotating speaker creates a very complex effect, with a sinusoidal volume shift (tremolo) trailing a sinusoidal pitch shift (vibrato). Meanwhile, the rotating speaker is throwing the sound all over the speaker cabinet and the room, creating a reverb effect that changes character at the rotation rate.

That’s one rotating speaker. A Leslie cabinet has two, a rotating speaker for treble and a rotating baffle around a bass speaker. They run at different speeds. Also, you can run the cabinet in either fast or slow mode. With the two speakers adjusting to mode changes at different rates of acceleration. Did I mention the effect of the room it’s in?

I digress

I think that simulating a Leslie on a microcontroller is possible. One speaker at one speed doesn’t seem so tough — I think you can adjust the main timer interrupt on a sine wave to effect the vibrato. The tremolo is a volume adjustment 90 degrees out of phase. Use a 90 degree offset into your sine table or use a recursive sine/cosine generator to calculate them at the same time.

Adding in the Leslie’s second speaker makes things more difficult. Since they run independently from each other, you can’t just tweak the timer interrupt to get vibrato. At least we already know the exact frequency of each tonewheel, so separating the bass and treble frequencies is just a matter of handling them in two groups.

You’ll need phase-adjustable all-pass filters for the two vibrato effects, and a model of speaker acceleration when you’re switching speeds. Full Leslie simulation is probably not a task for the same microcontroller that’s simulating the organ, but my gut feeling is that one might manage a two-speaker simulation alone.

Roto

Time to get down to business. roto is a project to simulate one manual of a Hammond B-3. It runs on an Arduino board with the MidiVox shield.

The Arduino uses an ATmega328 as its microcontroller, running at 16MHz. This is only enough power to run and mix about a third of the available tonewheels. Depending on your drawbar settings, it can play anywhere from three to 30 keys at the same time.

Here are a few highlights of the development process:

Choosing a sample rate

I knew from tonewheel tables that I would need to produce tones up to about 6000 Hz. Using this as my Nyquist Frequency left me needing to use a sample clock of at least 12000 Hz. I already had the code from bleep bloop that used a 15625 Hz sample clock, so I reused that. Tweaking that clock for a slightly longer loop is one place I could gain a few cycles.

Including the time it takes to update the DAC, the sample interrupt handler is running about 9% of the time:

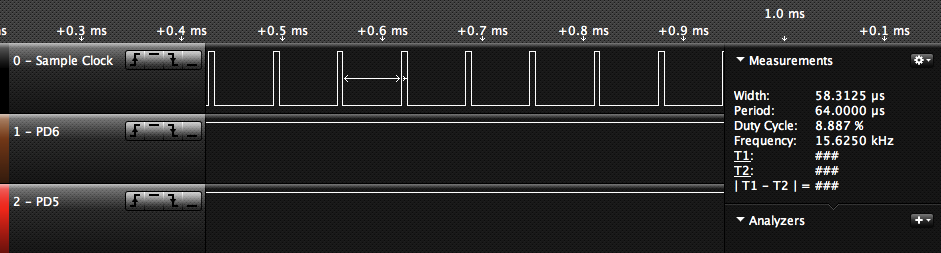
This leaves a 58 µs window to advance oscillators, mix them together according to the drawbars, and produce a sample.

Let’s see how long it takes to update the 91 oscillators, to know how much time remains for handling MIDI changes and mixing outputs together.

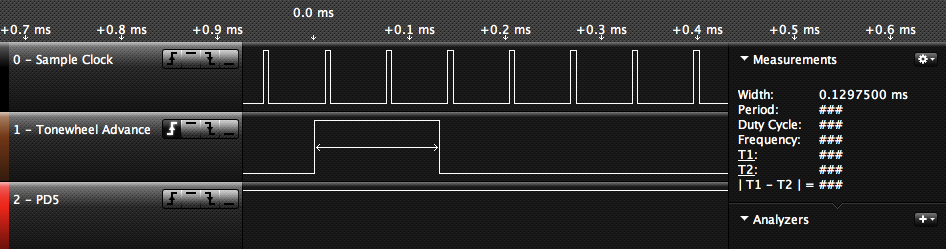
Oh.

This is advancing the oscillators, not figuring out which are active or scaling them by the drawbar volumes. Advancing 91 oscillators takes 130 µs, just over twice as long as our time slice. I’m going to have to get a little more clever.

Roto does a couple of things to work around the problem. Clearly the most important task is to have the next sample ready by the time its interrupt fires. If that doesn’t happen, you can’t update the DAC in time and you’ll have unintended frequency shifts.

In fact, having the next sample available is even more important than responding to the user. I don’t have to handle MIDI changes on every interrupt tick. I could handle them every 512 ticks and still have only 30 ms latency. That’s still instantaneous, as far as our brains are concerned. Roto keeps two 256-sample buffers and fills each after it is emptied, keeping the latency for MIDI changes around 15 ms.

Being able to keep the same list of “on” oscillators for multiple samples is a huge benefit. I can calculate each oscillator’s contribution to all the samples in the buffer in one shot, keeping the oscillator’s 16-bit position in two registers. That only needs to be saved to memory after calculating the full buffer.

I haven’t mentioned the impact of memory access on these calculations — a load or save of an oscillator’s 16-bit position is four cycles. A single oscillator update is:

1. load 16-bit oscillator position (4 cycles)
2. load 16-bit oscillator rate (4 cycles)
3. add them together (2 cycles)
4. shift the oscillator position to get an 8-bit index (1 cycle)
5. look up that value in the sine table (2 cycles)
6. add that value to the current 16-bit sample (2 cycles)
7. save 16-bit oscillator position (4 cycles)
8. save 16-bit current sample (4 cycles)

23 cycles, or 1.4 µs at 16 MHz.

Calculating the oscillator’s impact on the buffer at once, I avoid the four cycles in 1., 2. and 7. for all the mid-buffer samples. If I calculate 256 samples at a time, this is a savings of 3060 cycles every time the buffer fills. 52% of the total, worth saving for sure.

Volume

So far I’ve neglected the impact of the drawbar settings. On a Hammond, each click of the drawbar is a 3 dB gain in volume, up to eight clicks. 6 dB of gain is a doubling of volume, so we need an extra binary bit of scale factor for every two clicks available. So the drawbars map to a 4-bit multiplier. In the current code, I’m using a Q4.3 format number to maximize bit usage and get close to that 16x multiplier (Q4.3 gives us 15.875x).

I also need to think about the overall scale. So far I’m doing the same thing as the previous post — accumulating 16-bit samples and shifting them down to 12 bits before output. With an 8-bit sine table, we have enough headroom to play 256 (2¹⁶ / 2⁸⁾ oscillators at once. Excellent.

If each drawbar is pulled out all the way, the oscillators are scaled by a factor of 16 (the Q4.3 multiplier above). I have enough volume to play (2¹⁶ / 2⁸ / 16) oscillators at once. That’s only 16, not enough to play two keys. Uh oh.

Once I run out of headroom on volume, some samples overflow to meaningless values. This screws with the output waveform and creates an unpleasant sort of distortion.

This is a problem I haven’t solved yet.

It would be easy to give the samples more bits, either 24 or 32, but time is tight already. I could add a curve for dynamic range compression, but so far I haven’t thought of a good way to do that quickly enough. The Hammond has a behavior called “loudness robbing” that results in compression as a single tonewheel is played via multiple keys. Simulating that could help.

The oscillators can run in the background as long as they’re calculated in time for the sample clock. What if I offload them to additional microcontrollers?

Tonewheel coprocessors

A possible next move is to move oscillator generation onto separate chips. If I split the 91 oscillators into three groups and run the coprocessors at 20MHz, I should have time to spare.

The main microcontroller controls the system, handling MIDI messages and the final mix. Partitioning the oscillators carefully would leave the bass and treble sounds separated for two-speaker Leslie simulation.

Plus, I get to say tonewheel coprocessors. Tonewheel coprocessors.

I’m sure it would be productive to try a more powerful microcontroller. A 16-bit PIC or 32-bit ARM would probably suffice, running at a higher clock rate, and the ARM in particular would provide plenty of volume headroom.

Status

Where is roto now? It’s a decent sounding simulation of a Hammond:

1. It runs all 91 tonewheels, at rates calculated from the Hammond B-3’s original gear ratios.

2. It supports foldback properly at either end of the manual.

3. All nine drawbars are modeled accurately.

4. It has clicks on key presses that sound a lot like Hammond key click.

5. It supports the “complex tonewheels” of the bass pedals (though not the pedals' separate drawbars).

6. I have support for percussion on a branch, but I’m not going to merge that until I hash out the bigger issues.

The bigger issues

1. Each drawbar you pull out at all drastically reduces the number of notes you can play at once. At the moment that’s due to distortion when overflowing the 16-bit samples, but computation speed becomes limiting as soon as that’s solved.

2. No attenuation of higher frequency tonewheels.

3. No built-in effects, i.e. chorus and vibrato.

4. No Leslie!